
Archives
All posts for the month February, 2021
Find the Center of a Circle Using Only a Pencil and Straight Edge
I bought a wood lathe recently, and the first time I tried to center some wood, I went through the painful process of remembering how to find the center of a circle. This, despite having had three years of mechanical drawing classes.

Starting with a pencil and straight edge:
- Mark a line on the straight edge that’s a little more than 3/4 of the diameter (height) of the circle. It doesn’t have to be exact.
- Make a mark (M) at the top of the circle. The location of the mark need not be exact.
- Align the straight edge so that the corner is on mark M, and the line on the straight edge touches the right edge of the circle. Draw a line (A) from somewhere above the center of the circle out to it’s edge.
- Repeat on the left side, drawing line B.
- From where line B ends, line up the straight edge so that its corner sits on the end of line B, and its line touches the lower-right-hand edge of the circle. Draw line C along the straight edge, crossing the vertical center line.
- Repeat from the end of line A to the lower-left-hand edge of the circle, and draw line D
- At this point, lines C and D should form an “X” near the bottom of the circle.
- Draw a vertical center line (E) by aligning the straight edge with mark M and the intersection of lines C and D. Start the line above the center, and go all the way to the bottom edge.
- At this point, line E passes through the center vertically, but we need to find the horizontal center.
- From where line E touches the bottom of the circle, align the straight edge so that it crosses line A, and the line on the straight edge touches the upper-right-hand edge of the circle. Draw line F, crossing line A.
- Repeat this on the left side, crossing line B, and drawing line G.
- At this point, there should be an “X” on the left formed by lines B and G, and one on the right formed by lines A and F.
- Align the straight edge across the intersections of the left (B,G) and right (A,F) intersections, and draw the horizontal center line H.
The center of the circle is at the intersection of the vertical (E) and horizontal (H) center lines.
How This Works
Let’s call the distance from the corner of the straight edge to its mark S.
Let’s call the points where the horizontal center line meets the circle’s edges H1 (left) and H2 (right), and the point where the vertical center line meets the bottom V.
If we start at M and walk clockwise around the circle, we would pass through the points as follows: M (start) → H2 → V → H1 → M (back to start).

If the radius is 1, then the diameter is 2, and the length of MH2 is 1.41. We initially selected S to be about 3/4 of the diameter, or about 1.5.
The circle’s radius, R, is 1/2 the length of MV or H1H2. The length of MH2 would be √ R2 + R2 , and the same is true for H2V, VH1, and H1M.
If we assume that the radius R is “1 unit” (the actual length is irrelevant), then √ 12 + 12 = √ 2 , or about 1.41.
If the radius R = “1 unit” then the diameter = 2 ⋅ R = “2 units”.
By selecting S such that S is 3/4 of the diameter, 3/4 ⋅ 2 = 1.5. Since S>1.41, and we make two consecutive S-length marks around the circle, we know for a fact that 2 ⋅ S is greater than the length of MH2V.
By doing this twice, once clockwise, and once counterclockwise, we get lines C and D. We can call their intersection point T
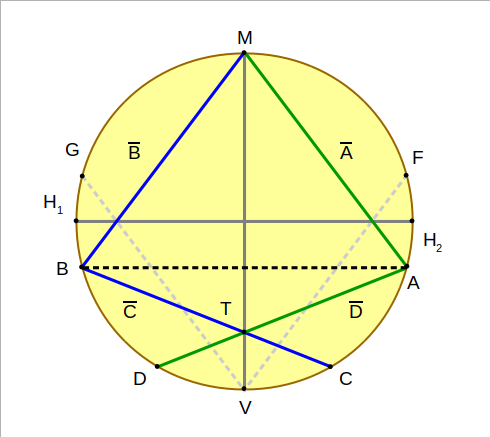
MAD = MBC = 2⋅S. Point T is located at the intersection of lines C and D. Triangles ΔMAT and ΔMBT are congruent. MT bisects AB.
⋅
It’s easy to prove that this forms two congruent triangles: ΔMAT and ΔMBT. If the line MT is the base of both, then because they are congruent, the height of both are the same, which means that MT perfectly bisects AB).
Since this line MT also bisects the equilateral triangle ΔMAB which is inscribed within the circle, that line must pass through the center of the circle as well.
Carrying MT out to the edge of the circle gives us point V.
By drawing a line from V of length S to the edge, we get line F, which crosses line A. We can call this intersection point U.

Points U and W are at the intersections of A and F, and B and G respectively. MUV is equilateral because MU=UV. MUV is congruent to MWV.
If we knew where the center of the circle (point O) was located, we could make the congruent triangle argument, that ΔMUO is congruent to ΔVUO, and just as with the vertical center line bisecting ΔMAB, UO would perfectly bisect the larger equilateral triangle ΔMUV.
On the other side, we draw line G of length S, which crosses line B at point W. Same congruency argument: ΔMWO is congruent to ΔVWO, and WO bisects equilateral triangle ΔMWV.
Because MU = VU we know that ΔMUV is equilateral, and the same for ΔMWV. Further, because of the congruency argument, we know that MU = MW and VU = VW, and therefore ΔMUV is congruent to ΔMWV.
If line UO bisects triangle ΔMUV, then it must intersect MV exactly at its center. Same for WO and triangle ΔMWV.
Therefore, WU passes through the center of both triangles at point O, where WU intersects MV.
And therefore, point O must be at the center of the circle, because VO = MO, and we know that MV passes through the center of the circle.
Note that this trick ONLY works if the the mark on the ruler (distance S) is > 1.41 times the radius.